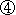を選ぶことになります。１割の生徒がこの誤答を選んでいました。
| （１） | イ 符号を間違えて 1/3−2/3＝−1/3 としたと思われるものや，割り算よりも引き算を先に計算したために答えが −2/9 となったと思われるものがたくさんありました。 |
|---|---|
| エ ｘ2 と ｘ3 を掛けて ｘ6 とした人がかなりいました。イ もそうですが，今一度，計算の仕方を確認しましょう。 | |
| （２） | 割とできていました。直接 x，y に代入して計算した人と，x2−y2＝(x＋y)(x−y) と因数分解してから x，y に代入して計算した人が半々ぐらいでした。 |
| （３） | ａ2−ｂ2＝(ａ＋ｂ)(ａ−ｂ) を利用する因数分解の問題です。まぎらわしい選択肢がないせいか，よくできていました。 |
| （４） | 両辺に 6 をかけて分母を払うときに，右辺の 1 を 6 倍するのを忘れ，そのままにして計算すると 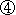を選ぶことになります。１割の生徒がこの誤答を選んでいました。
|
| （５） | 左辺の式を展開し整理してしまい，因数分解できなくて戸惑った人もいたようですが，割とできていました。2 次方程式の解の公式を知っていて，使っていた人もいました。 |
| （６） | a：b＝m：n ならば an＝bm （内側の積は外側の積に等しい） |
| （７） | (変化の割合)＝(y の増加量)／(x の増加量) より，−2＝(ｙ の増加量)／4 |
| （８） | 思っていた以上に出来ていませんでした。正確に計算できるように練習しましょう。検算も忘れずに！ |
| （１） | ｎ角形の内角の和は 180゜×(ｎ−2) です。 |
|---|---|
| （２） | 5 人から 2 人を選ぶ方法は ab，ac，ad，ae，bc，bd，be，cd，ce，de の 10 通り，このうち c を含む選び方は ac，bc，cd，ce の 4 通りです。 |
| （３） | 24/a が整数となるような a の値は，24 の正の約数 8 個の他に，−6 や 1/2 など他にもたくさんあります。 |
| （１） | 展開図を書いて考えます。側面の扇形の中心角を a゜ とすると，扇形の弧の長さと底面の円周の長さが等しいことから，2π×9×(ａ/360゜)＝2π×5 ∴ ａ＝200゜ よって求める表面積は S＝(側面積)＋(底面積)＝π×92×(200゜/360゜)＋π×52 ちなみに，円錐の表面積について 「底面の円の半径を r，母線の長さを l，表面積を S とすると，S＝πr(r＋l )」 が成り立ちます。 |
|---|---|
| （２） | 「１つの弧に対する円周角の大きさは，その弧に対する中心角の半分である。」 言いかえると，「１つの弧に対する中心角の大きさは，その弧に対する円周角の２倍である。」 したがって，図から，2ｘ＋80゜＝360゜ |
| （３） | DC//FE より AF：FD＝AE：EC＝2：4＝1：2 なので FD＝5×2/3＝10/3 ∴ BG：GE＝BD：DF＝5：10/3＝15：10＝3：2 |
| （４） | △ABD に三平方の定理を用いると，BD2＋62＝102 ∴ BD＝8 BC＝ｘ とおくと，AC＝ｘ，CD＝8−ｘ なので，△ACD に三平方の定理を用いると，(8−ｘ)2＋62＝ｘ2 |
| （１） | 放物線 ｙ＝ａｘ2 上に点 (4，8) があるので， ｘ＝4 のとき ｙ＝8 ∴ 8＝ａ×42 |
|---|---|
| （２） | 3 点 P，Q，R の ｙ 座標はそれぞれ 0，(1/2)ｔ2，8 となるので，PQ＝(1/2)ｔ2，QR＝8−(1/2)ｔ2 したがって，PQ：QR＝1：3 より 3PQ＝QR 3×(1/2)ｔ2＝8−(1/2)ｔ2 この方程式を解いて，ｔ＝2 (∵ ｔ＞0) したがって Q の ｙ 座標は (1/2)×22＝2 |
| （３） | 求める直線は辺 OA の中点 (−2，4) と点 Q(2，2) を通ります。 |
| （２） | X＝29ｘ＋319 より 29ｘ＝X−319 X が偶数なので X−319 は奇数，したがって 29ｘ も奇数となり，ｘ が奇数であることがわかります。4 つの数は小さい順に書き入れているので，11＜ｘ＜23 よって ｘ＝21 |
|---|---|
| （３） | 4 つの整数の中でいちばん小さい整数を ｎ とすると， X＝ｎ(ｎ＋1)＋(ｎ＋2)(ｎ＋3)＋ｎ(ｎ＋2)＋(ｎ＋1)(ｎ＋3)＝4ｎ2＋12ｎ＋9＝(2ｎ＋3)2 ｎは整数なので 2ｎ＋3 も整数 したがって X は整数 2ｎ＋3 の平方に等しい。 |